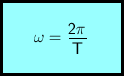
K popisu pohybu po kružnici se kromě klasické rychlosti používá i tzv. úhlová rychlost. Tato rychlost je definována jako opsaný úhel (v radiánech) za stanovenou dobu. Čas jednoho oběhu nebo-li perioda je obvykle značen T. Jeden oběh odpovídá velikosti úhlu 2·π radiánů.
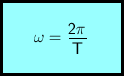
ω ... úhlová rychlost
π ... Ludolfovo číslo (3,14159...)
T ... perioda (doba oběhu)
Předpokládá se, že těleso (v ideálním případě hmotný bod) s danou úhlovou rychlostí se pohybuje po kruhové dráze s daným poloměrem. Aktuální (okamžitá) poloha tělesa se vyjádří v systému pravoúhlých souřadnic:
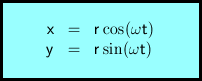
t ... čas
x ... x-ová souřadnice
y ... y-ová souřadnice
r ... poloměr
ω ... úhlová rychlost
Složky rychlosti získáme derivací dle času t. Složky vx a vy dohromady vytváří vektor okamžité rychlosti, který má tečný směr ke kruhové trajektorii.
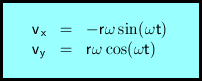
t .... čas
vx ... x-ová složka vektoru rychlosti
vy ... y-ová složka vektoru rychlosti
r .... poloměr
ω .... úhlová rychlost
Pro velikost vektoru rychlosti získáme:
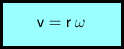
v ... rychlost (velikost vektoru rychlosti)
r ... poloměr
ω ... úhlová rychlost
Dalším derivováním dle času t získáme složky vektoru okamžitého zrychlení. To směřuje do středu kruhové trajektorie. Nazývá se tedy dostředivé zrychlení.
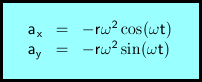
t .... čas
ax ... x-ová složka vektoru zryhlení
ay ... y-ová složka vektoru zrychlení
r .... poloměr
ω .... úhlová rychlost
Pro velikost dostředivého zrychlení z výše uvedeného tedy plyne:
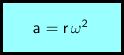
a ... dostředivé zrychlení (velikost vektrou zrychlení)
r ... poloměr
ω ... úhlová rychlost
URL: https://www.walter-fendt.de/phcz/circularmotion_math_cz.htm
Walter Fendt, 4. srpna 2007
Poslední změna: 24. listopadu 2013